penalty algorithm

One of the ways of replacing a constrained optimization problem with an unconstrained one is by adding a penalty function to the objective function that depends - in some logical way - on the value of the constraints.

The idea is to minimize a sequence of unconstrained minimization problems where the infeasibility of the constraints is minimized together with the objective function.

Following text was taken from http://mdolab.utias.utoronto.ca/aer1415.html:

4.2 Penalty and Barrier Methods

One of the ways of replacing a constrained optimization problem with an unconstrained one is by adding a penalty function to the objective function that increases depending on the value of the constraints.

There two main types of penalization methods: penalty functions impose a penalty for violating a constrain, and barrier methods other imposes a penalty for reaching the boundary of an inequality constraint.

4.2.1 The Quadratic Penalty Method

This is the simplest type of penalty function. The new objective function will be the original one plus a term for each constraint, which is positive when the current point violates the constraint and zero otherwise.

Consider the equality-constrained problem:

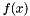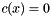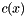minimize $f(x)$ subject to $c(x) = 0$ where $c(x)$ is an m-dimensional vector whose j-th component is 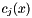$c_j(x)$. We assume that all functions are twice continuously differentiable.

We require a penalty for constraint violation to be a continuous function 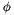$\phi$ with the following properties

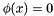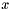$\phi(x) = 0$ if $x$ is feasible

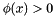$\phi(x) > 0$ otherwise,

The new objective function is

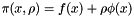$\pi(x, \rho) = f(x) + \rho\phi(x)$, (4.22)

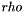were $rho$ is positive and is called the penalty parameter. The quadratic penalty function is defined as

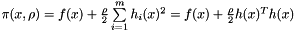
$\pi(x, \rho) = f(x) + \frac{\rho}{2} \sum\limits_{i=1}^m h_i(x)^2 = f(x) + \frac{\rho}{2}h(x)^Th(x)$

Algorithm:

  1. Check termination conditions. if 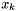$x_k$ satisfies the optimality conditions, he algorithm terminates successfully.
  2. Minimize the penalty function. With 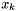$x_k$ as the starting point, execute an algorithm to solve the unconstrained subproblem minimize 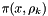$\pi(x, \rho_k)$ w.r.t. 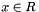$ x \in R $ and let the solution of this subproblem be $x_{k+1}$.
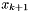  3. Increase the penalty parameter. Set 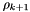$\rho_{k+1}$ to a larger value than 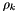$\rho_k$, set k = k + 1 and return to 1.

About "penalty_factor" parameter

penalty_factor is a parameter that used for special gridding rules like leq, geq, mean, wmean, hist and other of this kind. These gridding rules adds some condition and causes surfit for using penalty algorithm. Each of these gridding rules have additional parameter called "penalty_factor". This parameter sets how fast the penalty parameter 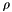$\rho$ should be changed.

It is recomended to set penalty_factor from -3 to 3, but for most cases the default value for penalty_factor should be usable.


surfit: gridding and contouring software.