Functions | |
| bool | completer (REAL D1=1, REAL D2=2, REAL alpha=0, REAL w=1) |
| bool | completer_add (REAL weight=1, REAL D1=1, REAL D2=2, REAL alpha=0, REAL w=1) |
| bool | value (const char *val="undef") |
| bool | value_add (REAL weight=1, REAL val=0) |
| bool | mean (REAL value, REAL penalty_factor=-2) |
| boolvec * | wmean (REAL value, const char *surface_name="*", REAL penalty_factor=-2) |
| bool | leq (REAL value, REAL penalty_factor=0) |
| bool | geq (REAL value, REAL penalty_factor=0) |
| boolvec * | hist (const char *histogram_name="*", REAL penalty_factor=-1, size_t treshold=5) |
Detailed Description
Function Documentation
| bool surfit::completer | ( | REAL | D1 = 1, |
| REAL | D2 = 2, |
||
| REAL | alpha = 0, |
||
| REAL | w = 1 |
||
| ) |
- Tcl syntax:
- completer D1 D2
- Description:
- This rule describes the resulting surface behavior in the areas of low data density. This rule applies to whole resulting surface. Here is simple example of "completer" D1 and D2 variables influence:
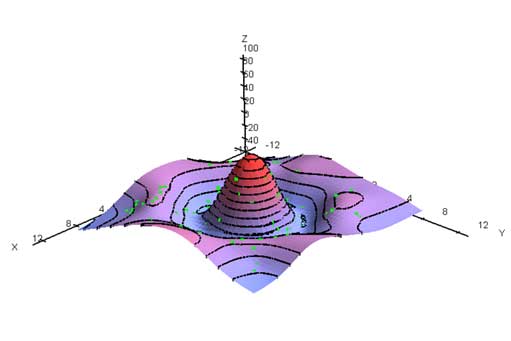completer 0 1
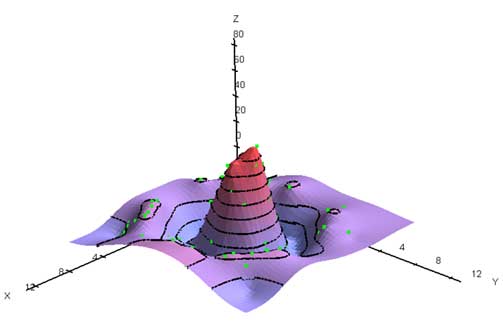completer 1 5
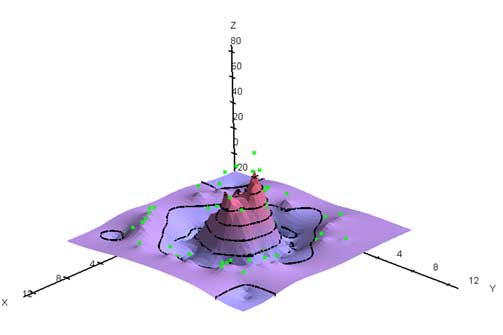completer 1 0
- Parameters
-
D1 weight coefficient for rule that the resulting surface should tend to constant surface D2 weight coefficient for rule that the resulting surface should tend to plane surface alpha anisotropy angle (degrees) w anisotropy factor
- Math:
- This command adds the following functional to the functional sequence:
where![\[ \Phi(u_{1,1},\ldots,u_{N,M}) = D_1 \Phi_1(u_{1,1},\ldots,u_{N,M}) + D_2 \Phi_2(u_{1,1},\ldots,u_{N,M}), \]](form_126.png)
![\[ \Phi_1(u_{1,1},\ldots,u_{N,M}) = \left[ \sum\limits_{j=0}^{M-1} \sum\limits_{i=0}^{N-2} \left( \frac{ u_{i+1,j} - u_{i,j} } { h_x } \right)^2 + \sum\limits_{i=0}^{N-1} \sum\limits_{j=0}^{M-2} \left( \frac{ u_{i,j+1} - u_{i,j} } { h_y } \right)^2 \right] \]](form_127.png)
![\[ \Phi_2 = \left[ \sum\limits_{j=0}^{M-1} \sum\limits_{i=0}^{N-3} \left( \frac{ u_{i+2,j} - 2u_{i+1,j} + u_{i,j} } {h_x^2} \right)^2 + \right. \]](form_128.png)
![\[ 2\sum\limits_{j=0}^{M-2} \sum\limits_{i=0}^{N-2} \left( \frac{ (u_{i+1,j+1} - u_{i,j+1}) - (u_{i+1,j} - u_{i,j}) } { h_x h_y } \right)^2 + \]](form_129.png)
![\[ \left. \sum\limits_{i=0}^{N-1} \sum\limits_{j=0}^{M-3} \left( \frac{ u_{i,j+2} - 2u_{i,j+1} + u_{i,j} } { h_y^2 } \right)^2 \right]. \]](form_130.png)
| bool surfit::completer_add | ( | REAL | weight = 1, |
| REAL | D1 = 1, |
||
| REAL | D2 = 2, |
||
| REAL | alpha = 0, |
||
| REAL | w = 1 |
||
| ) |
- Tcl syntax:
- completer_add weight D1 D2
- Description:
- This function modifies previous (modifiable) rule by adding the completer rule with some weight. This rule applies to whole resulting surface.
- Parameters
-
weight informational weight for this rule D1 weight coefficient for rule that the resulting surface should tend to constant surface D2 weight coefficient for rule that the resulting surface should tend to plane surface alpha anisotropy angle (degrees) w anisotropy factor
| bool surfit::geq | ( | REAL | value, |
| REAL | penalty_factor = 0 |
||
| ) |
- Tcl syntax:
- geq value penalty_factor
- Description:
- This rule adds the surface condition - "the resulting surface should be greater than or equal to value".
- Parameters
-
value resulting surface values should be lower than or equal to this real number penalty_factor parameter for penalty algorithm
- Math:
- This command adds the condition:
where (i,j) - indices of the cells, z - constant value![\[ u_{i,j} \geq z, \]](form_73.png)
| boolvec* surfit::hist | ( | const char * | histogram_name = "*", |
| REAL | penalty_factor = -1, |
||
| size_t | treshold = 5 |
||
| ) |
- Tcl syntax:
- hist "histogram_name" penalty_factor threshold
- Description:
- This rule adds the surface condition - "the resulting surface histogram should be equal to given histogram".
- Parameters
-
histogram_name desired histogram penalty_factor parameter for penalty algorithm treshold another parameter for changing if something going wrong :)
- Math:
- This command adds the condition:
where histeq is the histogram equalization algorithm described in the book R. Gonzalez and R. Woods Digital Image Processing, Addison-Wesley Publishing Company, 1992, Chap. 4.![\[ u_{i,j} = histeq( u_{i,j} ), \]](form_132.png)
| bool surfit::leq | ( | REAL | value, |
| REAL | penalty_factor = 0 |
||
| ) |
- Tcl syntax:
- leq value penalty_factor
- Description:
- This rule adds the surface condition - "the resulting surface should be lower than or equal to value".
- Parameters
-
value resulting surface values should be lower than or equal to this real number penalty_factor parameter for penalty algorithm
- Math:
- This command adds the condition:
where (i,j) - indices of the cells, z - constant value![\[ u_{i,j} \leq z, \]](form_72.png)
| bool surfit::mean | ( | REAL | value, |
| REAL | penalty_factor = -2 |
||
| ) |
- Tcl syntax:
- mean value penalty_factor
- Description:
- This rule adds the surface condition - "the resulting surface mean value should be equal to real number".
- Math:
- This command adds the condition:
where (i,j) - indices of the cells, Q - total number of cells, m - desired mean value![\[ \frac {\sum\limits_{i,j} u_{i,j}} {Q} = m \]](form_86.png)
| bool surfit::value | ( | const char * | val = "undef" | ) |
- Tcl syntax:
- value val
- Descrpition:
- Using this rule the resulting surface approximates constant value. This rule applies to whole resulting surface.
- Parameters
-
val real number for surface approximation. Also you may set val to "undef" string to fill surface with undef_value values.
- Math:
- This command adds the following functional to the functional sequence:
![\[ \Phi(u_{1,1},\ldots,u_{N,M}) = \sum_{i,j} \left( u_{i,j} - z \right)^2, \]](form_125.png)
| bool surfit::value_add | ( | REAL | weight = 1, |
| REAL | val = 0 |
||
| ) |
- Tcl syntax:
- value_add weight val
- Description:
- This function modifies previous (modifiable) rule by adding the value rule with some weight. This rule applies to whole resulting surface.
- Parameters
-
weight informational weight for this rule val real number for surface approximation
- Math:
- This command modifies previous functional
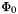by adding 
:
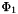where![\[ \Phi(u_{1,1},\ldots,u_{N,M}) = \Phi_0(u_{1,1},\ldots,u_{N,M}) + w\Phi_1(u_{1,1},\ldots,u_{N,M}), \]](form_65.png)
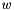- informational weight, ![\[ \Phi_1(u_{1,1},\ldots,u_{N,M}) = \sum_{i,j} \left( u_{i,j} - z \right)^2, \]](form_131.png)
| boolvec* surfit::wmean | ( | REAL | value, |
| const char * | surface_name = "*", |
||
| REAL | penalty_factor = -2 |
||
| ) |
- Tcl syntax:
- wmean value "surface_name" penalty_factor
- Description:
- This rule adds the surface condition - "the resulting surface weighted mean value should be equal to real number".
- Math:
- This command adds the condition:
where (i,j) - indices of the cells,![\[ \frac {\sum\limits_{i,j} z(x_i,y_j) u_{i,j}} {z(x_i,y_j)} = m \]](form_87.png)
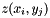- weighted surface value for the (i,j) cell, m - desired weighted mean value