Functions
for contours
surfit gridding rules

Functions

boolvec * contour (const char *cntr_name="*")
 
boolvec * contour_add (REAL weight=50, const char *cntr_name="*")
 
boolvec * smooth_contour (const char *cntr_name="*", REAL penalty_factor=0)
 
boolvec * contour_leq (const char *cntr_name="*", REAL penalty_factor=0)
 
boolvec * contour_geq (const char *cntr_name="*", REAL penalty_factor=0)
 

Detailed Description

Function Documentation

boolvec* surfit::contour ( const char *  cntr_name = "*")
Tcl syntax:
contour cntr_name
Description:
Using this rule the resulting surface approximates contour values.
Parameters
cntr_namecontour name
Math:
This command adds the following functional to the functional sequence:

\[ \Phi(u_{1,1},\ldots,u_{N,M}) = \sum_i \sum_j \left( u_{i,j} - z_{i,j} \right)^2, \]

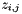where (i,j) - indices of the cells cross with contour, $ z_{i,j} $ - contour mean value for the (i,j) cell.
boolvec* surfit::contour_add ( REAL  weight = 50,
const char *  cntr_name = "*" 
)
Tcl syntax:
contour_add weight cntr_name
Description:
This rule modifies a previous (modifiable) rule by adding the contour rule with some weight. Use this rule if you don't know contour values exactly. Using this rule the resulting surface approximates contour taking into account a previous (modifiable) rule.
Parameters
weightinformational weight for this rule
cntr_namecontour name
Math:
This command modifies previous functional 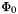$ \Phi_0 $ by adding $ \Phi_1 $:

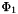\[ \Phi(u_{1,1},\ldots,u_{N,M}) = \Phi_0(u_{1,1},\ldots,u_{N,M}) + w\Phi_1(u_{1,1},\ldots,u_{N,M}), \]

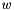where $ w $ - informational weight,

\[ \Phi_1(u_{1,1},\ldots,u_{N,M}) = \sum_i \sum_j \left( u_{i,j} - z_{i,j} \right)^2, \]

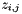where (i,j) - indices of the cells cross with contour, $ z_{i,j} $ - contour mean value for the (i,j) cell.
boolvec* surfit::contour_geq ( const char *  cntr_name = "*",
REAL  penalty_factor = 0 
)
Tcl syntax:
contour_geq cntr_name penalty_factor
Description:
This rule adds the surface condition - "the resulting surface at contour should be greater than or equal to contour values".
Parameters
cntr_namecontour name
penalty_factorparameter for penalty algorithm
Math:
This command adds the condition:

\[ u_{i,j} \geq z_{i,j} \]

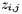where (i,j) - indices of the cells cross with contour, $z_{i,j}$ - contour mean value for the (i,j) cell
boolvec* surfit::contour_leq ( const char *  cntr_name = "*",
REAL  penalty_factor = 0 
)
Tcl syntax:
contour_leq cntr_name penalty_factor
Description:
This rule adds the surface condition - "the resulting surface at contour should be lower than or equal to the contour values".
Parameters
cntr_namecontour name
penalty_factorparameter for penalty algorithm
Math:
This command adds the condition:

\[ u_{i,j} \leq z_{i,j} \]

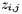where (i,j) - indices of the cells cross with contour, $z_{i,j}$ - contour mean value for the (i,j) cell
boolvec* surfit::smooth_contour ( const char *  cntr_name = "*",
REAL  penalty_factor = 0 
) 
\par Tcl syntax:
smooth_contour \ref str "cntr_name" penalty_factor

\par Description:
This rule tells surfit that resulting surface should approximate contour Z-values.
The result of approximation is that resulting surface should be very similar to given contours.
The main difference with \ref contour gridding rule is that resulting surface is
more smooth near contours. 

\param cntr_name \ref d_cntr "contour" \ref str "name"
\param penalty_factor parameter for \ref penalty

\par Math:

    Problem: we need to approximate contours (or isolines with different values) by adjusting

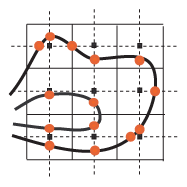
cell values. Let consider Figure 1: solid straight lines show cells borders, dot lines connect cells centers (black squares), thick black curves shows contours projection to the XoY plane. Red points on the figure are intersections of curves and dot lines. 

\image html matr_sect.gif

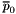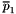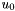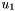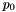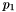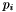Consider the case then the contours cross one of the dot lines, i.e. contours lay between two cells centers (see Figure 2). On the figure $\overline{p}_0$ and $\overline{p}_1$ are cells centers coordinates (X or Y), $u_0$ and $u_1$ are adjustable values for those cells. Red circles are points where contours cross vertical plane (this plane comes through points $p_0$ and $p_1$). $p_i$ - are points coordinates (X or Y), 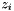$z_i$ - Z coordinates.

matr_sect2.gif

We are trying to approximate points 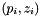$(p_i,z_i)$ with straight line. To do this we are going to find a minimum of the following functional:

\[ \Phi = \sum\limits_{i=1}^N \left( f(p_i) - z_i \right)^2 \rightarrow \min, \]

where

\[ f(p) = u_0 + (u_1-u_0) \frac{p-\overline{p}_0}{\overline{p}_1-\overline{p}_0}. \]

To solve our problem we should write this functional for each pair of neighbour cells, if at least one of contours lays between them.

For more details see f_cntr_smooth.tex


surfit: gridding and contouring software.